Product of Experts for Visual Generation - An Illustrated Example

At Wayfarer Labs, we want to create a real-time video generative model that generates physically plausible video games. However, it's not so easy to get away with training 1 video model to simulate every aspect of a video game faithfully, and, to that end, it could be prudent to compose multiple complementary models.

This blog post is breaking down one such framework, introduced in the Product of Experts for Visual Generation paper, that builds on the Product of Experts (introduced in this paper by Geoff Hinton) for Image/Video Generation. It proposes taking existing specialist models ("experts" at a particular domain) and incorporating their individual expertise by having them influence the diffusion sampling at inference time. We will use a toy example to illustrate this method, with an easy-to-follow Jupyter notebook provided at this Github repository.

If you’re new to diffusion/flow models:

The premise is that you’re trying to learn to generate images/videos by sampling from the image/video distribution, and you’re learning using some dataset that faithfully approximates that distribution (e.g. ImageNet).

In practice, while it's possible to sample from the Gaussian Distribution, it's intractable to sample from the image/video distribution that your dataset approximates (data curation aside!). To get around this, diffusion models and flow models are trained to help us map from a gaussian distribution to the image distribution.

Flow models do this by learning a “velocity field” that outputs the direction and magnitude that each pixel needs to move to continue on its path to map to the image distribution. They learn this by noising (then learning to denoise) an image from your dataset.

To “sample” an image using a flow model, you generate random gaussian noise and iteratively use the velocity output by the model to move it towards the image distribution (i.e. turn it into an image sample).

To learn more about diffusion/flow models, I find this video to be helpful. I would also highly recommend this video as it builds the right intuitions for understanding the product-of-experts paper’s formulations. Both videos, by the same uploader, are astoundingly well-made, and I highly recommend checking them out!

A proof-of-concept setting: colored point cloud sphere

Our simple example is centered around trying to sample from a spherical, colored point cloud. We are trying to turn a 256x6-dimensional noise into a 3 dimensional sphere made up of 256 RGB points. For each of the 256 points, the first 3 dimensions are an XYZ coordinate respectively, and the remaining 3 points are the RGB color values of that point.

This is the groundtruth image we are trying to reconstruct. Note that the colors can be an arrangement of any 3 random colors!

It’s trivial to teach a single model to flow random noise back into any color sphere that we sample, and can even be done analytically (instead of training any neural nets). For this blog post, however, we will be composing five separate models.

These will be four generative models (one for each spatial axis, and one for the color dimensions). Each spatial expert will only be able to see and flow along one axis, and will try (and fail, within the number of sampling steps provided to it) to reconstruct the full sphere. The color expert will flow the random colors of the gaussian noise to the mean of the colors present in the initial noised sample. If the average color is green, then the scattered points will get greener over time, and so on. We will also use a single reward model that rewards a particular point cloud for having more points of a chosen color.

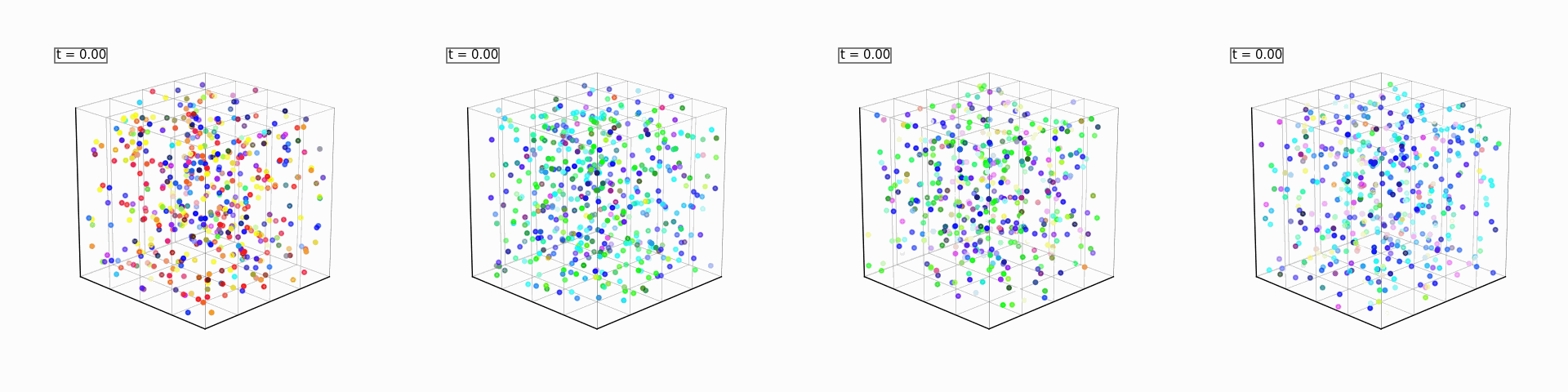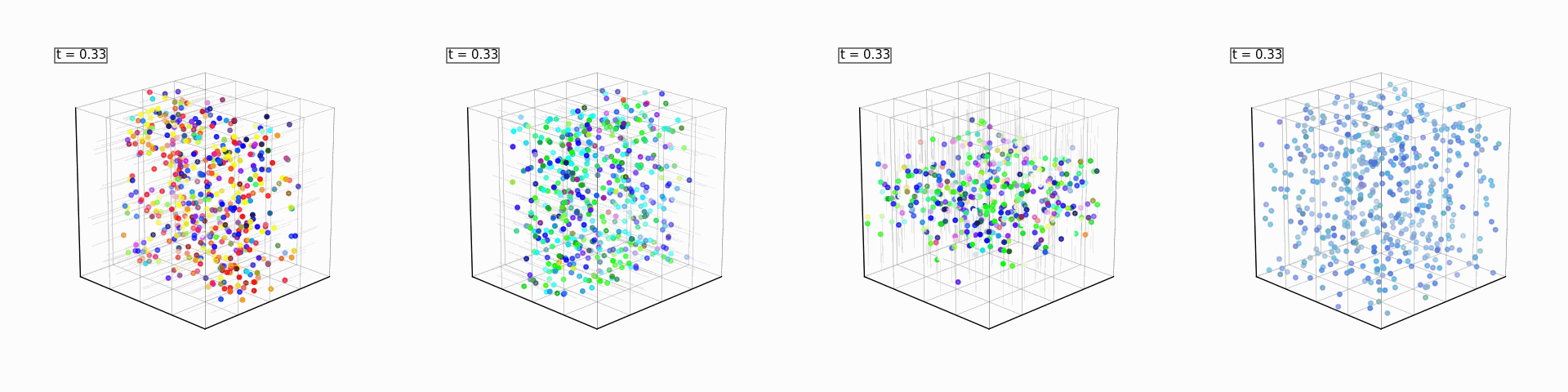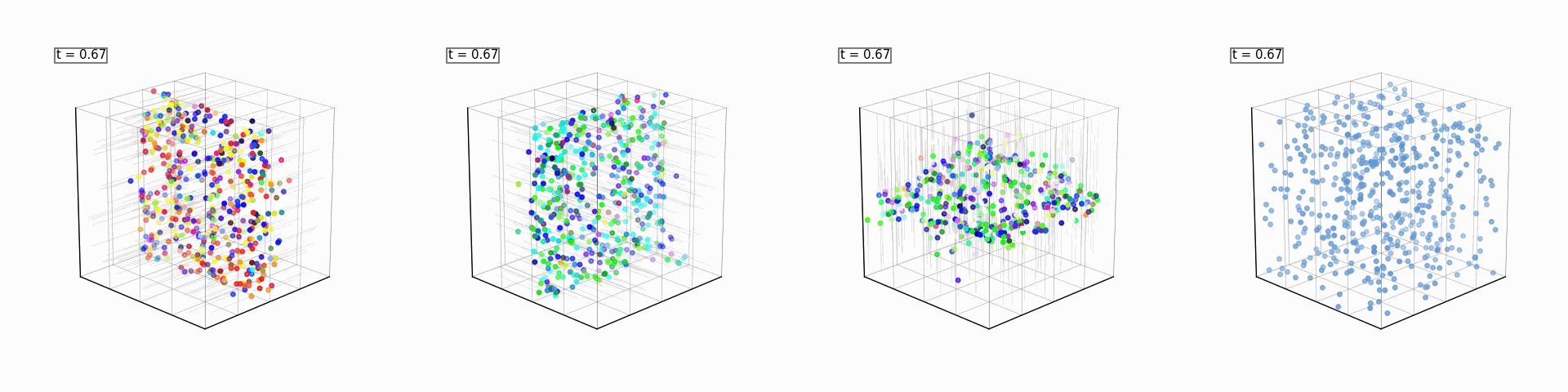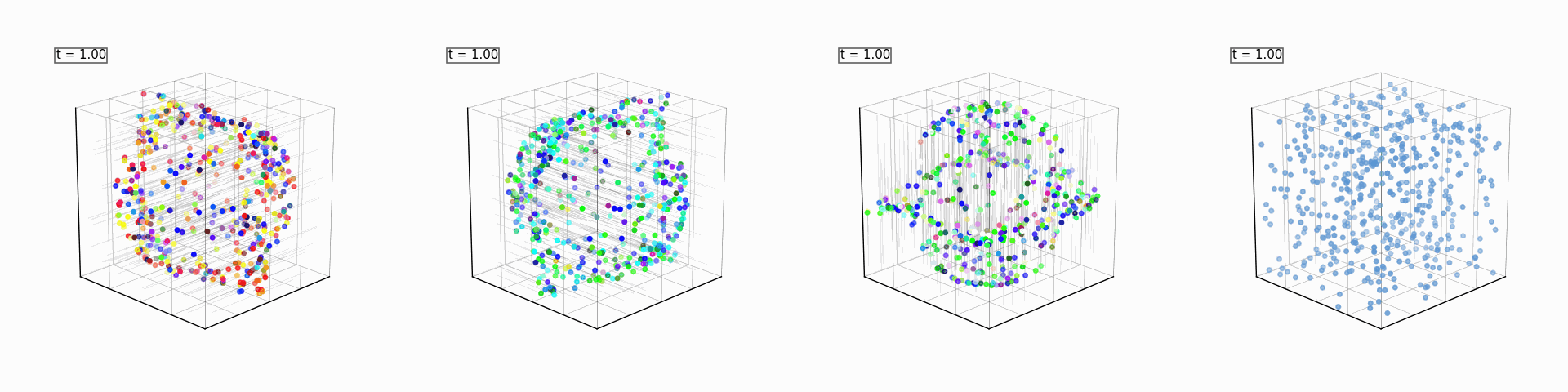
A small caveat about the color expert is that the sampled colors are not gaussian samples. If you are sampling 256 RGB pixels, you are virtually guaranteed that their average would be gray (0.5 on each R/G/B value on the unit gaussian). To really showcase Product of Experts for Visual Generation, we need (for this example) the mean to be discernable between noise samples. To get around this, we sample a tri-modal distribution with poles at 3 different colors pre-determined from a fixed color palette. Also, we use an analytical model that just calculates the velocity as the difference between our current noise’s color and the mean color (no gradient descent or neural nets for this expert).

Recap of the demo setting:

1) Three spatial generative models that flow random volumetric noise across only their chosen axis. Individually, these models cannot reconstruct the sphere without limitations.

2) A color-space analytical “model” that flows random colors to the mean of the initial noise. This can be interpreted as generative for the purposes of this demo.

3) A discriminative model that gives a positive reward for a sample proportional to how much of a chosen color it contains.

All of the above models will be combined to reconstruct the full sphere, and, with the discriminator as a reward model, steer the generation into a color of our choosing every time:

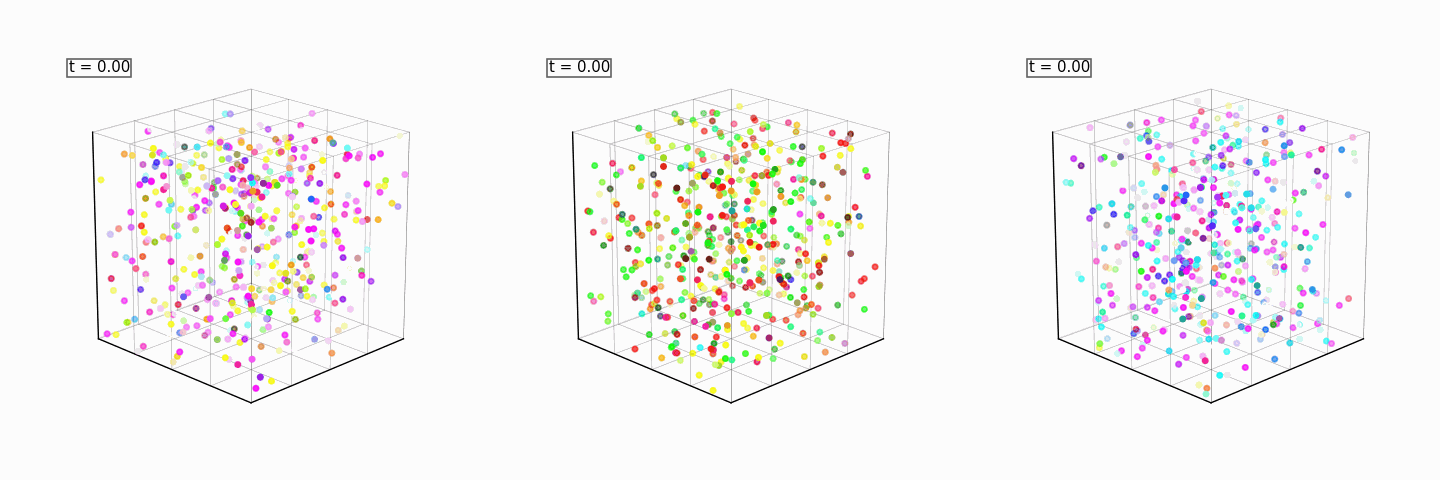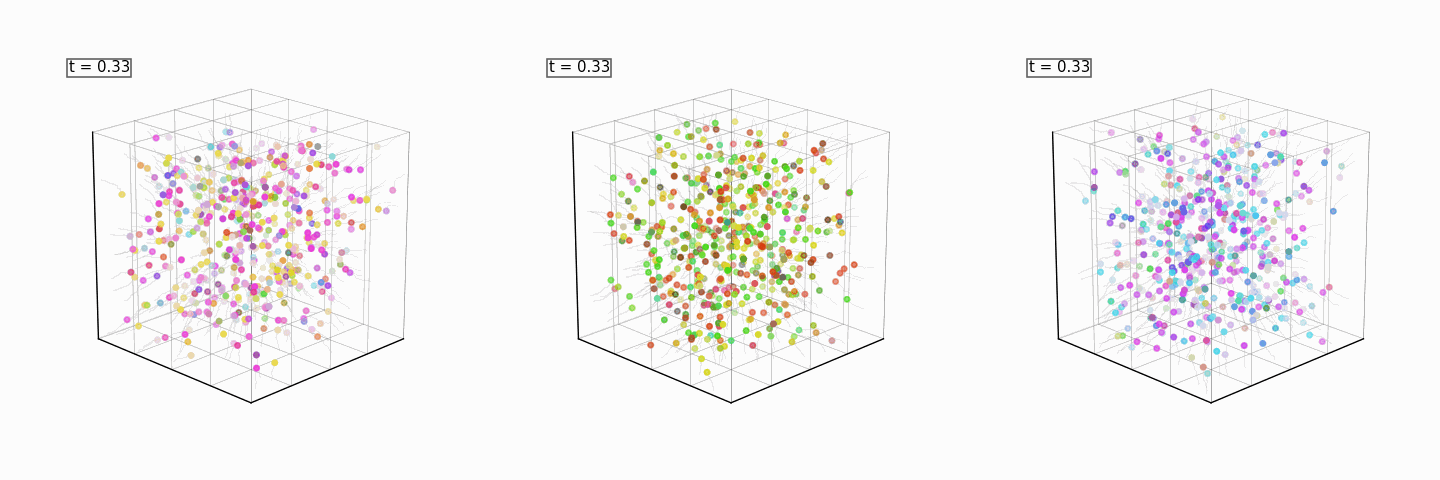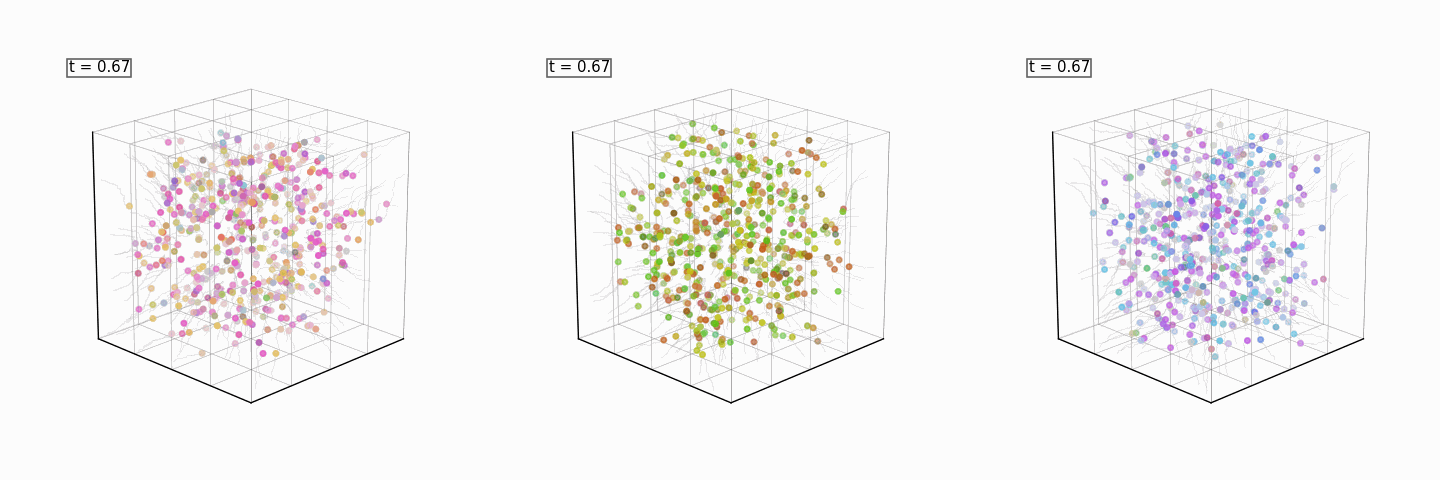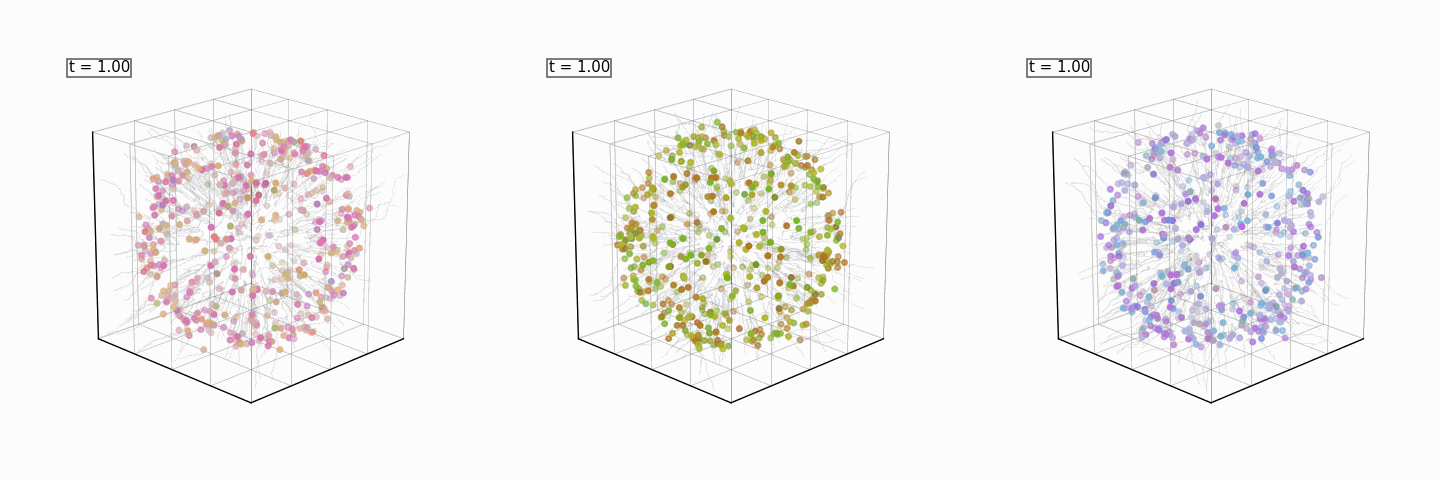
Product of Experts for Visual Generation:

For generating videos/images that adhere to multiple constraints (specified by multiple experts), you can just sample many images in parallel and discard all the ones that don’t fit all the constraints. This approach is called rejection sampling. As you can imagine, this is incredibly inefficient, because the larger the dimension you’re operating in, the lower the likelihood of sampling something that fits all constraints at once. Image and Video Generation is incredibly high dimensional, so this wouldn’t work.

The paper uses a more sample-efficient alternative: Annealed Importance Sampling (AIS). I will explain the components and intuitions behind it, and tie into diffusion/flow models, below.

Step 1: Sampling from a set of generative experts:

You want to draw a sample from a product of experts, and the distribution you’re sampling from should be proportional to the combined (via a product) distributions of each expert. A useful property is that this product concentrates probability mass in regions where all experts agree, which leads to a sharper overall distribution.

However, just because each individual expert’s distribution should integrate to 1, does not mean that their product would integrate to 1; because of the increased sharpness, we lose some total volume, and need to compute a normalization constant Z that we can then divide our resulting distribution by to restore the total volume to 1. Computing the normalization constant is intractable, so we can opt for alternate approaches for sampling from the product-of-experts distribution.

If you eyeball it, you can easily notice how the product of gaussians at the bottom does not integrate to 1

Markov chain Monte Carlo (MCMC) sampling:

To paraphrase Wikipedia, MCMC is a class of algorithms to sample from probability distributions that can’t be reasoned with analytically (e.g. you can’t compute their normalization constant). For this PoE for Video Generation paper, they use Langevin Sampling (or Gibbs sampling, for non-continuous models).

Langevin sampling goes as follows: for each timestep, you add the gradient of the log of your probability distribution to your sample, to get to the next sample. This means you are climbing in the direction that would increase the probability density of your sample.

This is equivalent to sampling from a diffusion model. The diffusion model is a neural net that learns to approximate the “gradient of the log probabilities” (i.e. outputs a score function). Flow models output a velocity, which is not the same as the score, but we can still convert between the two using some knowledge of our noise schedule.

If you play this out, however, the first issue is that this will eventually always end up exactly at the peak(s) of the distribution we are trying to approximate.

The second issue is that, from any local peak, there is no immediate direction we can move in that would immediately get us to the global maxima without first reducing our probability density. You only see a small slope around your current location in the probability landscape, so if every movement decreases the probability density, it’s optimal (according to MCMC as a whole) to not move anywhere.

Naive score following & mode collapse:

To get around the first issue, Langevin sampling injects a bit of random gaussian noise to each sampling step. Over time, this gets us centered around the local maxima, instead of directly at their peak. The gaussian noise is multiplied by the square-root of the step-size to scale it appropriately. This is because, in Brownian motion, the variance grows linearly with time, so the standard deviation grows linearly with the square root of time (or rather, our step-size epsilon). Our new equation now looks like this:

Screenshot taken from odie's whisper blog.

Annealed Sampling:

Earlier, we spoke about how the distribution of the product of experts is sharp, with high density only in areas where all experts agree. This creates multiple isolated modes of the product distribution (multiple peaks with very deep valleys between them).

This makes it very easy for MCMC sampling (such as Langevin), as a local sampling procedure, to get trapped at a local maxima. To get around this, the authors perform Annealed MCMC sampling, in which they refine the sample at each intermediate denoising step in the diffusion/flow process. For example, if we are performing diffusion sampling with T denoising steps, then each of those intermediate steps is its own distribution that is “smoother” because it is mixed with some gaussian noise. The intermediate distributions are easier to sample from, which in turn makes sampling from the product distribution (at timestep 1) more tractable.

Step 2: Parallel Sampling with Discriminative Experts:

In step 1, we have seen how to sample from the product of generative experts using Annealed MCMC Sampling, since we have access to a score function. However, lots of experts don’t afford us a score function, but are still very useful (e.g. classifiers, physics engines, etc.) In this section, we will break down how the PoE for Visual Generation paper handles this.

To formulate this section, we can just multiply the product of generative experts with product of discriminative experts. To adapt this to Annealed Sampling, we simply take multiply by the product of discriminative experts on the intermediate sample:

Screenshot taken from the Product of Experts for Visual Generation paper (equation 6)

Importance Sampling for experts without a score:

To incorporate discriminative experts with annealed sampling, we can use “importance sampling” (since we don’t have access to a score). To do this, you sample L samples from the product of generative experts as done in step 1, re-weight each sample by how important it is to the product of discriminative experts, and then re-sample according to that distribution.

MCMC and auto-correlation:

There’s one glaring issue with this; if you start from the same sample in the MCMC sampling, and do L independent rollouts, then each of your L samples will be correlated with each other (as they start from the same point in the landscape). Due to the challenging landscape of the product-of-generative-experts, these L samples will still have poor coverage of the distribution, and plain importance sampling will not work.

Sequential Monte Carlo sampling for discriminative experts:

To get around this, you sample L particles at the start of annealed sampling (and not MCMC sampling), and maintain them over the course of denoising across all T timesteps. At the end of each denoising timestep (right after the MCMC refinement), you re-weigh and re-sample, effectively culling out intermediate generations with poor agreement with the discriminative experts:

Combining both steps gives you the Annealed Importance Sampling that the paper introduces. I have placed the algorithm below. A code implementation can be found here.